\\\\(
\nonumber
\newcommand{\bevisslut}{$\blacksquare$}
\newenvironment{matr}[1]{\hspace{-.8mm}\begin{bmatrix}\hspace{-1mm}\begin{array}{#1}}{\end{array}\hspace{-1mm}\end{bmatrix}\hspace{-.8mm}}
\newcommand{\transp}{\hspace{-.6mm}^{\top}}
\newcommand{\maengde}[2]{\left\lbrace \hspace{-1mm} \begin{array}{c|c} #1 & #2 \end{array} \hspace{-1mm} \right\rbrace}
\newenvironment{eqnalign}[1]{\begin{equation}\begin{array}{#1}}{\end{array}\end{equation}}
\newcommand{\eqnl}{}
\newcommand{\matind}[3]{{_\mathrm{#1}\mathbf{#2}_\mathrm{#3}}}
\newcommand{\vekind}[2]{{_\mathrm{#1}\mathbf{#2}}}
\newcommand{\jac}[2]{{\mathrm{Jacobi}_\mathbf{#1} (#2)}}
\newcommand{\diver}[2]{{\mathrm{div}\mathbf{#1} (#2)}}
\newcommand{\rot}[1]{{\mathbf{rot}\mathbf{(#1)}}}
\newcommand{\am}{\mathrm{am}}
\newcommand{\gm}{\mathrm{gm}}
\newcommand{\E}{\mathrm{E}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\mU}{\mathbf{U}}
\newcommand{\mA}{\mathbf{A}}
\newcommand{\mB}{\mathbf{B}}
\newcommand{\mC}{\mathbf{C}}
\newcommand{\mD}{\mathbf{D}}
\newcommand{\mE}{\mathbf{E}}
\newcommand{\mF}{\mathbf{F}}
\newcommand{\mK}{\mathbf{K}}
\newcommand{\mI}{\mathbf{I}}
\newcommand{\mM}{\mathbf{M}}
\newcommand{\mN}{\mathbf{N}}
\newcommand{\mQ}{\mathbf{Q}}
\newcommand{\mT}{\mathbf{T}}
\newcommand{\mV}{\mathbf{V}}
\newcommand{\mW}{\mathbf{W}}
\newcommand{\mX}{\mathbf{X}}
\newcommand{\ma}{\mathbf{a}}
\newcommand{\mb}{\mathbf{b}}
\newcommand{\mc}{\mathbf{c}}
\newcommand{\md}{\mathbf{d}}
\newcommand{\me}{\mathbf{e}}
\newcommand{\mn}{\mathbf{n}}
\newcommand{\mr}{\mathbf{r}}
\newcommand{\mv}{\mathbf{v}}
\newcommand{\mw}{\mathbf{w}}
\newcommand{\mx}{\mathbf{x}}
\newcommand{\mxb}{\mathbf{x_{bet}}}
\newcommand{\my}{\mathbf{y}}
\newcommand{\mz}{\mathbf{z}}
\newcommand{\reel}{\mathbb{R}}
\newcommand{\mL}{\bm{\Lambda}}
\newcommand{\mnul}{\mathbf{0}}
\newcommand{\trap}[1]{\mathrm{trap}(#1)}
\newcommand{\Det}{\operatorname{Det}}
\newcommand{\adj}{\operatorname{adj}}
\newcommand{\Ar}{\operatorname{Areal}}
\newcommand{\Vol}{\operatorname{Vol}}
\newcommand{\Rum}{\operatorname{Rum}}
\newcommand{\diag}{\operatorname{\bf{diag}}}
\newcommand{\bidiag}{\operatorname{\bf{bidiag}}}
\newcommand{\spanVec}[1]{\mathrm{span}{#1}}
\newcommand{\Div}{\operatorname{Div}}
\newcommand{\Rot}{\operatorname{\mathbf{Rot}}}
\newcommand{\Jac}{\operatorname{Jacobi}}
\newcommand{\Tan}{\operatorname{Tan}}
\newcommand{\Ort}{\operatorname{Ort}}
\newcommand{\Flux}{\operatorname{Flux}}
\newcommand{\Cmass}{\operatorname{Cm}}
\newcommand{\Imom}{\operatorname{Im}}
\newcommand{\Pmom}{\operatorname{Pm}}
\newcommand{\IS}{\operatorname{I}}
\newcommand{\IIS}{\operatorname{II}}
\newcommand{\IIIS}{\operatorname{III}}
\newcommand{\Le}{\operatorname{L}}
\newcommand{\app}{\operatorname{app}}
\newcommand{\M}{\operatorname{M}}
\newcommand{\re}{\mathrm{Re}}
\newcommand{\im}{\mathrm{Im}}
\newcommand{\compl}{\mathbb{C}}
\newcommand{\e}{\mathrm{e}}
\\\\)
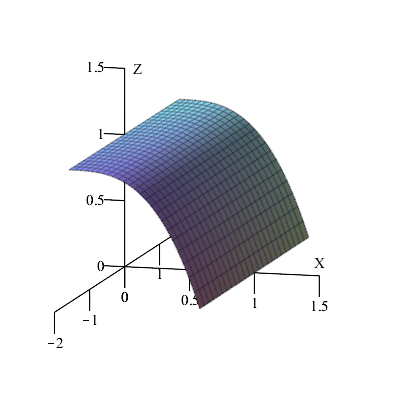
Exercise 1: Flux through an Open vs. Closed Surface A function $\,h:\reel^2 \rightarrow \reel\,$ is given by the expression
$$\,h(x,y)=1-x^3\,.$$
We consider a rectangle in the $(x,y)$ plane that is determined by $\,0\leq x\leq 1\,$ and $\,-\frac{\pi}2\leq y\leq \frac{\pi}2\,.$ Let the surface $\,\mathcal F\,$ be the part of the graph of $\,h\,$ that is located vertically above the rectangle.
A
Provide a parametric representation of $\mathcal F\,.$
Show hint
Note that $\mathcal F$ is a graph surface.
Show answer
$$\mathbf s(u,v)=(u,v,1-u^3)\quad\text{where}\quad u\in \left[0,1\right]\,,\,v\in \left[-\frac{\pi}2,\frac{\pi}2\right]$$
A vector field $\,\mV\,$ is given by
$$\,\displaystyle{\mV(x,y,z)=\begin{matr}{c}xz\newline x\cos(y)\newline 3x^2\end{matr}\,.}$$
B
Compute the flux of $\mV$ through $\mathcal F\,.$
Show hint
First find the integrand for the flux integral. It is a dot product.
Show hint
State from the parametric representation the normal vector $\mathbf N\,.$ Then the integrand is
$$\mV(\mathbf s(u,v))\cdot \mathbf N\,.$$
Show hint
The integrand is
$$-3u^6+3u^3+3u^2\,.$$
Show answer
$$\displaystyle{\int_{\mathcal F}}\mV\cdot \mathbf n\,\mathrm du=\frac{37}{28}\,\pi$$
Now let $\Omega$ denote a solid spatial region located vertically between the rectangle in the $(x,y)$ plane and $\mathcal F\,.$
C
Determine a parametric representation of $\Omega\,.$
Show hint
Probably you can use the parametric representation you made for $\mathcal F\,$ by adjusting the third coordinate a bit.
Show answer
$$\mr(u,v,w)=(u,v,w(1-u^3))\,\quad\,,\,u\in \left[0,1\right]\,,\,v\in \left[-\frac{\pi}2,\frac{\pi}2\right]\,,\,w\in \left[0,1\right]$$
D
Use Gauss’ Theorem to determine the flux of $\mV$ out through the surface of $\Omega\,.$
Show hint
Actually the surface of $\Omega$ consist of 5 parts. The good thing about Gauss’ Theorem is that we only need one integral, but it is a volume integral.
Show hint
You must compute the volume integral of the divergence of $\mV$ through $\Omega\,.$ Find the integrand, which is
$$\mathrm{Div}(\mV)(\mr(u,v,w))\cdot\mathrm{Jacobian}_{\mathbf r }(u,v,w)\,,$$
and determine the triple integral, possibly using Maple.
Show hint
The integrand is
$$\,u^6w-2u^3w+w+u^4\sin(v)-u\sin(v)\,.$$
Show answer
$$\,\displaystyle{\frac{9}{28}}\,\pi$$
Exercise 2: 12 Fluxes of Fields with Constant Divergence A spatial region $\Omega_1$ is a solid unit sphere centred at the origin, and another spatial region $\Omega_2$ is given by the parametric representation
$$\mr(u,v,w)=(u\cos(v),u\sin(v),u^2+w(1-u^2)\,)\,,$$
$$u\in \left[0,1\right]\,,v\in \left[-\pi,\pi\right]\,,w\in \left[0,1\right].$$
Their surfaces $\partial \Omega_1$ and $\partial \Omega_2$ are oriented with outwards-pointing unit normal vectors. In addition we are given the following six vector fields:
$$\begin{align*}
\mV_1(x,y,z)&=(1,2,3)\newline
\mV_2(x,y,z)&=\left(-x,\frac y2,-\frac z3\right)\newline
\mV_3(x,y,z)&=(x-yz,-2y+xz^2,3z+yx^3)\newline
\mV_4(x,y,z)&=(k_1,k_2,k_3)\newline
\mV_5(x,y,z)&=(y-x^3,3x^2y,25+10z)\newline
\mV_6(x,y,z)&=(2xz-2xy-z,z^3+y^2,-z^2)
\end{align*}$$
A
Compute the 12 fluxes
$$\mathrm{Flux}(\mV_i,\,\partial\Omega_j)\,,\,i=1..6\,,\,j=1..2\,.$$
Show hint
Compute the volume of $\Omega_1$ and $\Omega_2\,$ and then the divergence of each of the six vector fields.
Show hint
$$\mathrm{Vol}(\Omega_1)=\frac43\pi$$
$$\mathrm{Vol}(\Omega_2)=\frac {\pi}2$$
From Gauss’ Theorem it follows that the fluxes are found by multiplication of the volume with the divergence.
Exercise 3: Gauss’ Theorem and Divergence A parametrized spatial region $\Omega_{\mathbf r}$ in $(x,y,z)$ space has the parametric representation
$$\mr(u,v,w)=(u\cos(v),u\sin(v),w)\,,\,\,u\in\left[0,2\right]\,,\,\,v\in\left[0,\frac{\pi}{2}\right]\,,\,\,w\in\left[0,5\right]\,.$$
A
$\Omega_{\mathbf r}$ is a parametrization of a simple geometric object. Describe which, and find its volume by elementary geometric means.
Show answer
This is a quarter of a cylinder of revolution with a bottom radius of $2$ and a height of $5$ . The volume is thus
$$\mathrm{Vol(\Omega_{\mr})}=\frac14\pi \mathrm{radius}^2h=\,5\pi\,.$$
We are about the vector fields $\mU$ and $\mV$ informed that:
$$\mathrm{Div}(\mU)(x,y,z)=\pi\,\,\,\,\mathrm{and}\,\,\,\,\mathrm{Div}(\mV)(x,y,z)=yz\,.$$
B
Determine the fluxes
$$\,\displaystyle{\int_{\partial \Omega_{\mathbf r}}\mU\cdot \mathbf n_{\partial \Omega_{\mathbf r}}\,\mathrm du}\,\,\,\,\textrm{and}\,\,\,\,
\,\displaystyle{\int_{\partial\Omega_{\mathbf r}}\mV\cdot \mathbf n_{\partial \Omega_{\mathbf r}}\,\mathrm du}\,.$$
Show answer
$$\,\displaystyle{\int_{\partial \Omega_{\mathbf r}}\mU\cdot \mathbf n\,\mathrm du}=5\pi^2\,$$
$$\,\displaystyle{\int_{\partial\Omega_{\mathbf r}}\mV\cdot \mathbf n\,\mathrm du}=\frac{100}{3}$$
Exercise 4: Gauss’ Theorem Applied on an Open Surface! We are given the vector field
$$\mV(x,y,z)=(\e^y+\cos(yz),\e^z+\sin (xz),x^2z^2),\, (x,y,z)\in\reel^3$$
together with a hemi-spherical surface $F$ given by
$$x^2+y^2+z^2-4z=0\,\,\mathrm{and}\,\,z\leq 2\,.$$
A
Draw a sketch of $F$ using pen and paper.
Show hint
Complete the square to remove the single term from the equation. You’ll then see that we are dealing with the bottom half of a spherical shell centred at $(0,0,2)$ with a radius of $2$ .
$F$ is thought to be oriented with a unit normal vector field with negative $z$ coordinate. We wish to determine the flux though $F,$ but it turns out to be rather difficult to integrate over the surface $F\,$ since the vector field is a bit complicated. On the other hand it is not difficult to compute $\mathrm{Div}(\mV)(x,y,z)\,.$ So let us tune the problem to be solvable via Gauss’ Theorem. We will start by integrating the divergence of $\mV$ through the solid hemisphere $\Omega$ that fills $F$ .
B
Compute the flux of $\mV$ out through the surface $\partial \Omega$ of $\Omega$ by computing
$$\int_{\Omega}\mathrm{Div} (\mV)\, \mathrm d\mu\,.$$
Show hint
This is a usual volume integral with a Jacobian and all.
Show hint
Create a parametric representation of the solid sphere and compute its corresponding Jacobian. Then restrict the vector field to this parametrization.
Show hint
A possible parametrization is
$$\mr(u,v,w)=(u\sin(v)\cos(w), u\sin(v)\sin(w), u\cos(v)+2)$$
with fitting parameter intervals.
The Jacobian becomes $\,u^2\sin(v)\,.$
We have now computed the flux through a closed surface. But the hemi-spherical surface $F$ is open at the top! We have thus included the flux through the top even though it shouldn’t have been included - let’s find it and subtract it away.
C
Find a parametric representation of the circular disc that can cover the top of the hemisphere.
Show answer
$$\mathbf s(u,w)=(u\cos (w),u\sin(w),2),\quad u\in\left[ 0,2\right] ,\, w\in\left[0,2\pi\right] $$
D
Compute the flux through the circular disc.
Show hint
$$N_{\mathbf s}=(0,0,u)$$
E
Now state the flux through $F$ .
Show hint
Subtract the flux through the circular disc at the top from the total flux through the closed surface that was found via the divergence integration.
Show answer
$$\mathrm{Flux}(\mV,F)=-\frac{64\pi}{15}$$
We are given the vector field
$$\mV(x,y,z)=(x^3+xy^2,4yz^2-2x^2y,-z^3)$$
and the solid region
$$\Omega=\left\{ (x,y,z)\,|\, x^2+y^2+z^2\leq a^2\right\}\,.$$
A
Compute the flux of $\mV$ out through the surface $\partial \Omega$ of $\Omega\,.$
Show hint
$$\mathrm{Div}(\mV)(x_0,y_0,z_0)=x^2+y^2+z^2$$
Show answer
$$\mathrm{Flux}(\mV,\Omega)= \int_{-\pi}^{\pi}\int_0^{pi}\int_0^a\, u^4\,\sin (v)\,\mathrm du\,\mathrm dv\,\mathrm dw=\frac{4a^5\pi}{5}$$
We are given the vector field $\mV(x,y,z)=(2x,3y,-z)$ and the solid region
$$\Omega=\left\{ (x,y,z)\,|\,\left( \frac{x}{a}\right) ^2+\left( \frac{y}{b}\right) ^2+\left( \frac{z}{c}\right) ^2\leq 1\right\}\,.$$
A
Determine the flux of $\mV$ out through the surface $\partial \Omega$ of $\Omega\,.$
Show hint
$$\mathrm{Div}(\mV)(x_0,y_0,z_0)=4$$
Show hint
What is the consequence of the divergence being constant?
Show hint
$\Omega$ is a solid ellipsoid.
Show answer
$$\mathrm{Flux}(\mV,\Omega)= \mathrm{Div}(\mV)(x_0,y_0,z_0)\cdot\Vol_\Omega=\frac{16\pi}{3}abc$$