Exercise 1: Today’s Wetware Exercise
What is $\,\displaystyle{\sin\left(3\frac{\pi}{2}\right)}\,$?
Exercise 2: Angular Measures in Degrees and Radians
State the radian values that correspond to the angles $30^\circ, 60^\circ, 120^\circ, 135^\circ$ and $300^\circ$.
Draw the unit circle in an $(x,y)$ coordinate system centered at $(0,0)$. Draw points on the unit circle corresponding to the arc lengths
Which degree values do these angles in radians correspond to?
Exercise 3: Sine and Cosine
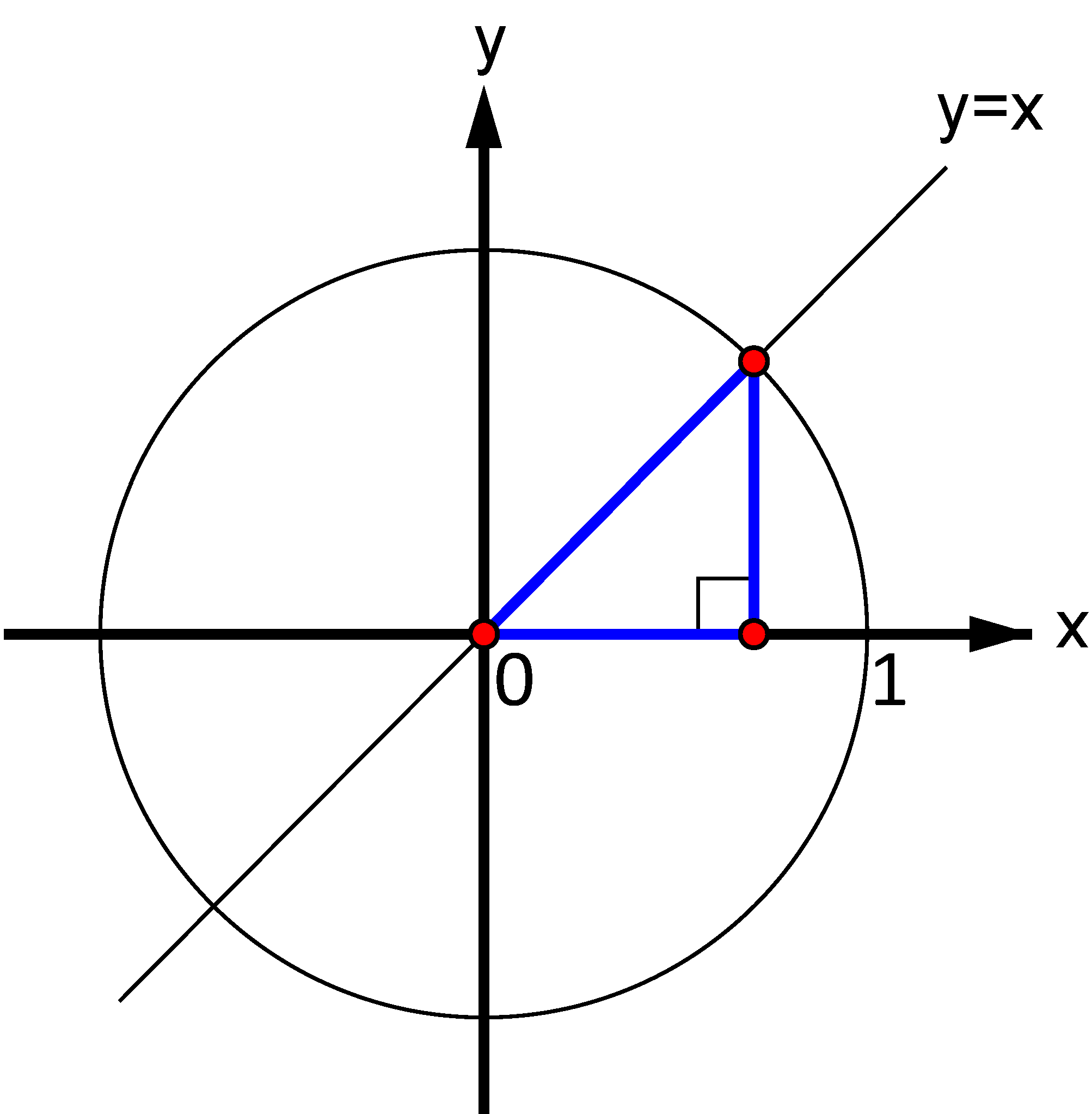
Use the figure (the blue triangle) to geometrically derive the exact values of $\,\displaystyle{\cos\left(\frac{\pi}{4}\right)}\,$ and $\,\displaystyle{\sin\left(\frac{\pi}{4}\right)}\,.$
Compute via symmetry considerations the values
Given $\,\displaystyle{\cos\left(\frac{\pi}{6}\right)}=\frac{\sqrt 3}{2}\,$ and $\,\displaystyle{\sin\left(\frac{\pi}{6}\right)}=\frac{1}{2}\,$, draw the point
on a unit circle and find by the use of symmetry considerations the numbers
For given numbers $\,A,\,b,\,C\,$ and $d$ the graphs of the functions
are plotted for $\,x\in \left[\,-\pi\,,\,\pi\,\right]\,$.
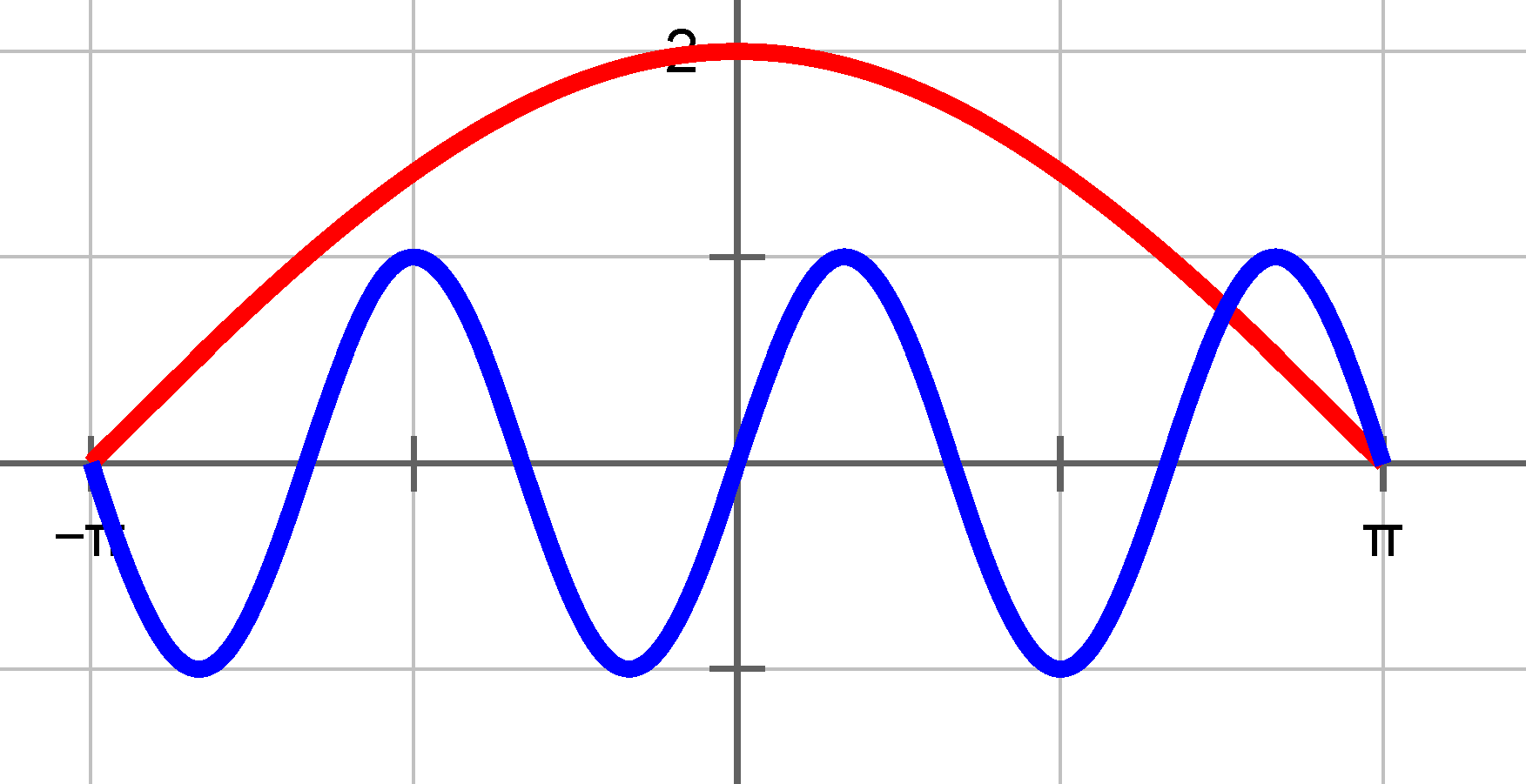
Determine the numbers $\,A,\,b,\,C\,$ and $d\,.$
Exercise 4: Polar coordinates
Given the numbers $z_0=1+i\sqrt{3}\,$, $z_1=-1+i\sqrt{3}\,$, $z_2=-1-i\sqrt{3}\,$ and $z_3=1-i\sqrt{3}\,$.
-
State the circle centered in $0$ at which the four numbers are located.
-
Compute $\,\arg(z_0)\,$ and then state the principal argument of $\,z_1\,,\,z_2\,$ and $\,z_3\,$. What are the polar coordinates of all four numbers?
A student needs to find the polar coordinates for the number $\,2-2i\,\,$. He chooses to use a calculator. By entering
he gets the absolute value $\,2\sqrt{2}\,.$ And by entering
he gets the argument $\,\displaystyle{\frac {\pi}4}\,.$
Check the calculations. What error has the student made?
Find the modulus and the principal argument of the following complex numbers:
-
$-2+2i$
-
$\displaystyle{-\frac{1}{6}+\frac{i}{2\sqrt{3}}}$
Three complex numbers are given by their polar coordinates like this:
Determine the rectangular form of the numbers.
Exercise 5: The Exponential Form of Complex Numbers
Write the following complex numbers on rectangular form:
The numbers $z_0=1+i\sqrt{3}\,$, $z_1=-\sqrt{3}+i\,$, $z_2=-1-i\sqrt{3}\,\,$ and $\,z_3=\sqrt{3}-i\,$ are given.
-
Convert the four numbers to exponential form.
-
Show that a binomial equation
were $w$ is a complex scalar, exists to which all four numbers are a solution.
Exercise 6: The Complex Exponential Function
The number $\,w=1-i\,$ is given.
-
Compute $|\,w\,|$ and $\hbox{Arg}(w)\,$.
-
Compute $|\,\e^w\,|$ and $\hbox{Arg}(\e^w)\,$.
Given the numbers $\,w_1=1\,,\,w_2=\e\,,\,w_3=i\,$ and $\,w_4=2i\,$, determine all solutions to the equations
where $\,n=1\ldots4\,$.
Determine all solutions to the equation
Show that $\,\e^z\neq0\,$ for all $\,z\in\mathbb C\,$.
Exercise 7: Geometric Addition and Multiplication
It is now time to install GeoGebra on your computer or to access it via a browser. See the link to GeoGebra on the Agenda of today.
When the software is ready, open the GeoGebra sheet komplekseTal. In this sheet, four complex numbers $\,z_1\,,\,z_2\,,\,z_3\,$ and $\,z_4\,$ are given. Construct the following complex numbers:
Draw using the vector tool (in the line box) the position vectors of the found complex numbers. You might want to colour them differently. Finally, draw the five yellow labels to the corresponding numbers.
Note: In this exercise you may choose your own level of ambition (or go step by step from the easiest to the hardest):
- Mild: Right click on the sheet and activate Grid. Choose Lock the grid in Configurations $\rightarrow$ Catch the point. Find via geometric considerations the wanted numbers and draw them with the point tool.
- Medium: Construct the wanted numbers with dedicated GeoGebra construction tools, e.g. Parallel displace by vector and Reflection in point.
- Challenging: Find the numbers purely from ruler and compass construction. You’ll find the compass tools in the circle toolbox. A ruler construction is done using relevant tools from the line toolbox.
Exercise 8: Double Angles (Advanced)
The formulas of double angles as they are called are the following:
Use the latter (along with the dummy rule $\cos(v)^2+\sin(v)^2 =1$) to determine $\cos\left(\frac{\pi}{8}\right)\,$ and $\sin\left(\frac{\pi}{12}\right)\,.$
Use the first result in a) to find $\sin\left(\frac{\pi}{8}\right)\,,\cos\left(\frac{3\pi}{8}\right)\,$ and $\,\sin\left(\frac{3}{8}\pi\right)\,$.
Similarly, use the second result in a) to find sine and cosine values of interesting angles on the form $\,\frac{p\pi}{12}\,.$
