Exercise 1: Today’s Wetware Exercise
Reduce $\,\displaystyle{\frac{2^{-1}\cdot 2^4\cdot (2^3)^{-2}}{2^{-5}}\,\,.}\,$
Exercise 2: Right-Angled Triangles
Given an arbitrary right-angled triangle. Show from the definition of cosine and sine that:
-
The cosine of an acute angle is the adjacent side divided by the hypotenuse.
-
The sine of an acute angle is the opposing side divided by the hypotenuse.
A right-angled triangle has the sides$\,a=1\,$, $b=\sqrt{3}\,$ and $c=2\,.$ What are the exact angles expressed in radians?
The important trigonometric formula
is in Denmark typically called idiotreglen, translating directly to the idiot rule or the dummy rule. Which mathematical explanations can be given for this unflattering name?
Exercise 3: Arccos, Arcsine and Trigonometric Equations
Compute the numbers
Let $A=\{x\in{\mathbb R}|\,x\in \left[\,0\,,\,2\pi\,\right]\}$ and $B=\{x\in\reel\,|\,x\in \left[\,-\pi\,,\,\pi\,\right]\}$.
Solve the equation $\,\displaystyle{\cos(x)=\frac{1}{2}}\,$ within each of the sets $\,A,\,B\,$ and $\,\Bbb R\,.$
Solve the equation $\,\displaystyle{\sin(x)=-\frac{\sqrt 3}{2}}\,$ within each of the sets $\,A,\,B\,$ and $\,\Bbb R\,.$
Solve the equation $\,\displaystyle{\mathrm e^{\,i\cdot v}= \frac{1}{2}-\frac{\sqrt 3}{2}\,i\,}\,$ within each of the sets $\,A\,$ and $\,B\,.$
Exercise 4: Computations with Powers
Rewrite the following expressions to numbers of the form $\,a^p\,$ where $\,a\,$ is a positve real number and $\,p\in \mathbb Z$:
Exercise 5: Powers of Complex Numbers
Given $z=1+i\,,$ compute the modulus and principal argument of $z$. Use this result to determine the modulii and principal arguments of $z^2\,,$ $z^5\,,$ $z^8\,,$ and $z^{-10}\,$. Finally, provide the rectangular form of $z^2\,,$ $z^5\,,$ $z^8\,,$ and $z^{-10}\,$.
Exercise 6: Binomial Equations
Solve the binomial equations
Sketch the solutions in the complex number plane.
Solve the binomial equations
-
$z^3=1$
-
$z^3=i$
-
$z^3=1+i$
and sketch the solutions in the complex number plane.
Exercise 7: Exponential Growth (Highschool Recap)
A set has, at $t=0$, the magnitude $b$ and grows $\,20\,\%\,$ per time unit. Determine the number $a$ such that the functional expression
can be considered to be a model for the growth.
Determine the growth rate and the percentage growth per time unit for the exponentially growing/decreasing functions given by the functional expressions:
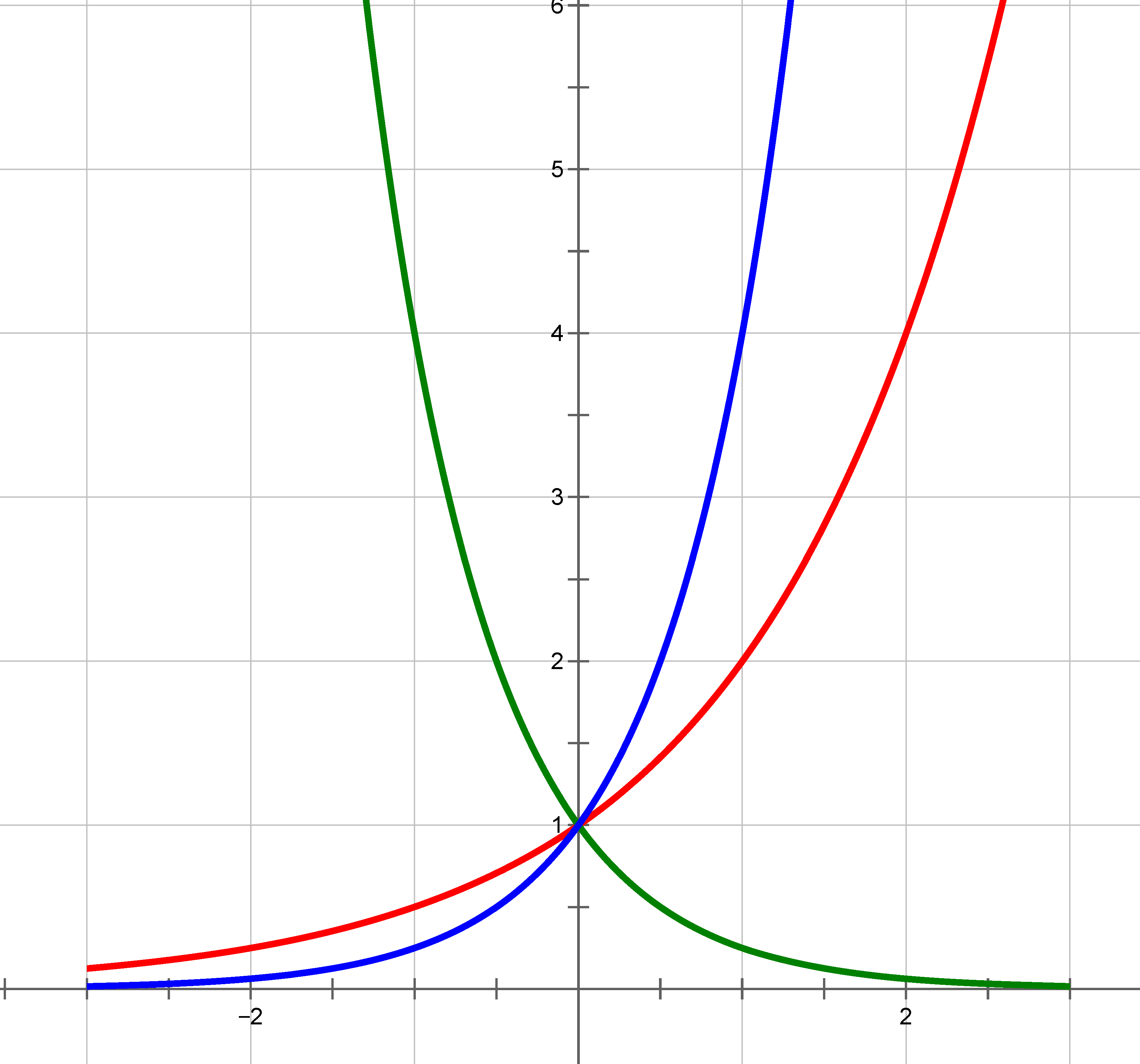
The figure below shows the graph of three exponential functions. State their base, and write each of them on the form
where $\e$ is the base for the natural exponential function and $k$ is a real number.